In the Bimaru puzzle you have to find hidden ships in a grid that is supposed to represent a part of the ocean. The goal is to logically exclude the locations where ships are placed. The numbers to the right and below indicate how many boxes in a row or column are occupied by ship parts. Ships may be horizontal or vertical, but may not touch each other, not even diagonally. Sometimes fields with water or ship parts are given to make the beginning easier. The most common puzzle size is 10×10 and includes a freighter, two yachts, three cutters and four dinghies.
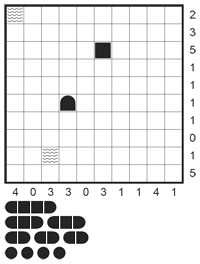
Basic Techniques
1. Fill in what you know for sure around given ship parts:
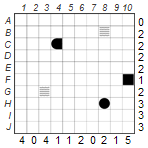
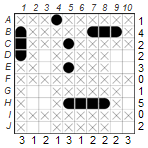
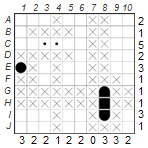
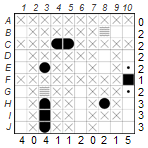
Let’s start with the puzzle below, in which three ship parts and two water fields are given. Since dinghies consist of only one element, all fields around H8 must be provided with an X for water. C4 contains the end piece of a ship, so there must be another part in C5. And because row C has a 2, the ship must be a cutter. Now we can enter the other end piece in C5 and add an X to the ten squares around the ship. F10 is a middle part, so it has to be a freighter or a yacht and it has to be vertical, because the middle part is directly at the grid. So the fields above and below are ship parts (marked by dots), and three more fields can be filled with water.
2. Mark any remaining boxes as water:
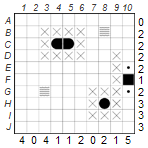
This technique is helpful when you have situations that can be clearly clarified. Row A and columns 2 and 7 have a default of 0, so all fields there can be provided with an X for water. In row C the two given fields are already occupied, so the rest can also get an X. And finally row F and the columns 4 and 5: You have 1 as default, so you can set an X in all remaining boxes.
3. Mark open fields as ship parts:
This technique helps to find out which free spaces must contain ship parts. Let’s look at column 3 with a 4 as a numeric default. Since there are exactly four spaces left, ship parts must be placed there. This means that in E3 a dinghy must be set and in H3, I3 and J3 a yacht. Now we can use technique 2 and add an X to the remaining fields.
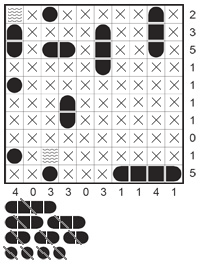
Advanced Techniques
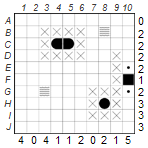
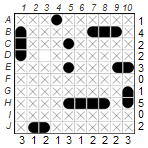
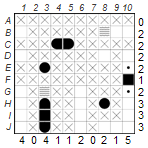
1. Remaining ships of a variety may be placed in only one way:
This technique is used when there is only one way to place all the remaining ships of a type. In our example there are only three cutters left to accommodate. However, there are seven possibilities: D3-E3, D10-E10, E9-E10, G3-H3, G10-H10, J2-J3, and J9-J10. Even though this may seem discouraging, some possible positions exclude others. For example, D10-E10 and E9-E10 are definitely mutually exclusive. On closer inspection, it becomes clear that there is only one way to place three cutters: E9-E10, G10-H10 and J2-J3. If you now set another dinghy in D3, the puzzle is solved.
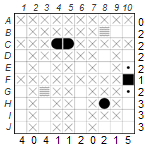
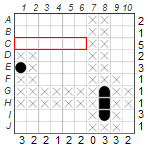
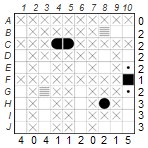
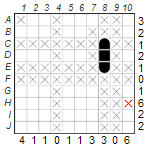
2. Several possible fields when placing a ship:
This technique is used when there is an overlap when placing ships. In the example below, the freighter consisting of four parts can only fit in row C. Even if there are different possibilities, the fields C3 and C4 will always contain parts of a ship and because we don’t know which parts of the freighter these are, we mark them with a dot for the time being.
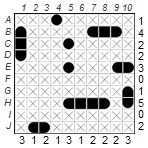
3. Indirect logic (process of exclusion):
Indirect logic can be applied in several ways to find out whether a field contains water or a ship part. In this example we would like to show that H10 is part of a ship and cannot contain water. Let’s assume that H10 could contain water and mark it with an X. According to basic technique 3, the rest of series H must contain two additional yachts, which would give us three yachts. But since there are only two yachts in the fleet, it is clear: H10 cannot contain water, but a part of a ship.
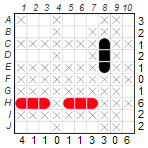
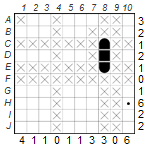
Good candidates for indirect logic are rows and columns in which exactly one water segment still has to be placed, as in row H in the example we have just investigated.